Bit Operations:
Before learning about bit operations, it is necessary to understand how to convert decimal to binary and binary to decimal. Here is a simple calculation method: to convert from right to left, multiply each number in binary by the corresponding power of 2. For numbers after the decimal point, convert from left to right.
- For example: How to convert binary to decimal
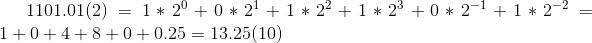
So, the general formula can be summarized as:
- For example: How to convert decimal to binary
To convert decimal integers to binary integers, use the method of division by 2 and taking remainders, in reverse order. The specific steps are as follows: divide the decimal integer by 2 to obtain a quotient and a remainder; then divide the quotient by 2 again to obtain another quotient and remainder, and so on, until the quotient is less than 1. Then, arrange the remainders obtained earlier as the least significant bits of the binary number, and the later remainders as the most significant bits, in order. For example: 255=(11111111)B
Left Shift <<:
10 << 1; //-> In binary, 10 is represented as 1010. Shifting left by 1 position gives 10100, which is then converted back to decimal as 20.
Right Shift >>:
13 >> 1; // -> In decimal, 13 can be seen as 12+1. In binary, 12 is represented as 1100. Shifting right by 1 position gives 110, which is then converted back to decimal as 6.
Bitwise Operations:
Bitwise AND:
The result is 1 only if each bit is 1, otherwise it is 0.
10 & 8; // -> 1010 & 1000 == 1000 -> 8
Bitwise OR:
The result is 1 if at least one bit is 1, otherwise it is 0.
10 | 8; // -> 1010 | 1000 == 1010 -> 10
Bitwise XOR:
The result is 1 only if each bit is different, otherwise it is 0.
15 ^ 5; // -> 1111 ^ 0101 == 1010 -> 10